A polygon has multiple straight sides. It can have three or more sides.
Polygons are closed figures that have multiple straight sides. The word “polygon” comes from two Greek words: “poly” meaning “many” and “gon” meaning “angle. ” Therefore, a polygon is a two-dimensional shape with many angles. A triangle, for example, is a polygon with three sides and three angles.
Polygons can have any number of sides greater than three, and each side connects to another to form a closed shape. Regular polygons have equal side lengths and angles, while irregular polygons have different side lengths and angles. Understanding the properties of polygons is essential in mathematics and geometry.
Credit: socratic.org
The Basics Of Polygons
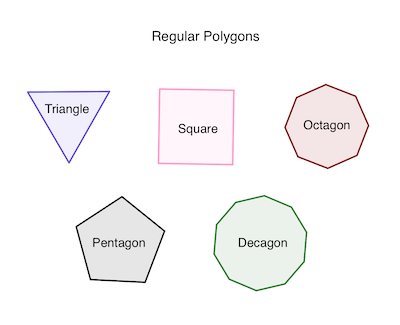
Learn the basics of polygons by understanding the number of sides each shape has. Polygons can have varying numbers of sides, with examples like triangles (3 sides), pentagons (5 sides), and hexagons (6 sides). Explore the world of polygons and their unique characteristics.
Defining Polygons
A polygon is a closed shape that consists of straight lines and has at least three sides. It is a fundamental concept in geometry and is commonly encountered in various real-world objects and structures. Polygons can be classified based on the number of sides they have, which range from three to infinity. Let’s explore some key characteristics of polygons.
Key Characteristics
1. Number of Sides:
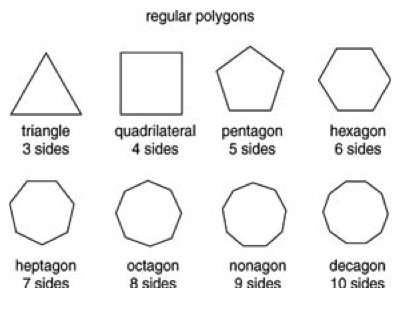
Polygons are defined by the number of sides they possess. The more sides a polygon has, the more complex its shape becomes. Common polygons include triangles (3 sides), quadrilaterals (4 sides), pentagons (5 sides), hexagons (6 sides), and so on. Understanding the number of sides helps us identify and classify different polygons.
2. Sum of Interior Angles:
One interesting characteristic of polygons is that the sum of their interior angles depends on the number of sides. To find the sum of interior angles in any polygon, we use the formula: (n-2) 180 degrees, where ‘n’ represents the number of sides. For example, a triangle has three sides, so its interior angles add up to (3-2) 180 = 180 degrees.
3. Regular vs. Irregular:
Polygons can be further classified as regular or irregular. A regular polygon has all sides of equal length and all angles of equal measure. Examples include equilateral triangles, squares, and regular hexagons. On the other hand, irregular polygons have sides and angles of different lengths and measures. Understanding the distinction between regular and irregular polygons helps us analyze geometric shapes more accurately.
4. Convex vs. Concave:
Another characteristic of polygons is whether they are convex or concave. A convex polygon has all interior angles less than 180 degrees and all sides lying on the same side of the polygon. It has a “bulging out” appearance and does not intersect itself. In contrast, a concave polygon has at least one interior angle greater than 180 degrees, and its sides may cross over each other. Recognizing the difference between convex and concave polygons is important when working with geometric figures.
5. Perimeter and Area:
The perimeter of a polygon refers to the total length of its sides, while the area is the measure of the space enclosed by the polygon. Calculating the perimeter and area of polygons is essential in various applications, such as architecture, engineering, and design. Different formulas are used depending on the type of polygon, making these calculations an important aspect of working with polygons.
Types Of Polygons
Regular Vs. Irregular
A regular polygon has equal sides and equal angles. An irregular polygon has sides and angles of different measures.
Simple Vs. Complex
A simple polygon is non-self-intersecting, whereas a complex polygon intersects itself. A simple polygon doesn’t cross itself, while a complex polygon has at least one crossing.
Understanding Sides
A polygon is a closed plane figure formed by joining three or more line segments. One of the key attributes of a polygon is the number of sides it has. Understanding the concept of sides in polygons is fundamental to grasping the nature of different shapes and their properties.
Minimum Sides Required
A polygon must have at least three sides. This is the minimum requirement for a shape to be classified as a polygon. Shapes with three sides are known as triangles, and they form the building blocks for more complex polygons. As the number of sides increases, the polygon takes on different names, such as quadrilaterals, pentagons, hexagons, and so on.
The Role Of Sides In Shapes
The sides of a polygon determine its overall structure and properties. The number of sides directly influences the internal angles of the polygon, which in turn affects its symmetry, area, and other geometric characteristics. Additionally, the type of polygon formed is determined by the number of sides it possesses, leading to a diverse range of shapes with unique attributes.
Infinite Possibilities
When we think of polygons, we often envision the common shapes we learn about in school, such as triangles, squares, and pentagons. However, the world of polygons extends far beyond these familiar forms. With an understanding of the concept of a polygon and the flexibility it offers, we can explore a vast array of shapes and sizes. Welcome to the world of infinite possibilities!
Beyond The Common Shapes
While triangles, squares, and pentagons are the most commonly known polygons, there are many more fascinating shapes to discover. These lesser-known polygons, known as N-gons, open up a world of creativity and mathematical exploration. An N-gon is simply a polygon with ‘N’ number of sides, where ‘N’ can be any whole number greater than or equal to three.
Let’s take a look at some examples of N-gons:
| Number of Sides | Name of Polygon |
|---|---|
| 4 | Quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| … | … |
As you can see, there is no limit to the number of sides a polygon can have. From a simple quadrilateral to a complex polygon with hundreds or even thousands of sides, the possibilities are endless.
Mathematical Formulas
In the study of polygons, mathematical formulas play a crucial role in understanding their properties and characteristics. Let’s explore the key mathematical formulas related to the sides and angles of polygons.
Calculating Internal Angles
When finding the sum of the internal angles of a polygon, the formula is (n-2) 180°, where ‘n’ represents the number of sides in the polygon.
Sides And Shape Dynamics
As the number of sides in a polygon increases, the shape dynamics become more complex. For instance, a triangle has 3 sides, a quadrilateral has 4 sides, and so on. The relationship between the number of sides and the shape dynamics is a fundamental aspect of polygon geometry.
Famous Polygons In History
The Pentagon
The Pentagon is a well-known pentagon with five sides.
The Hexagon In Nature
Hexagons are found in nature in beehives and snowflakes.
Polygons In Modern Use
Polygons are closed shapes with straight sides, and the number of sides can vary. A polygon must have at least three sides, but it can have many more, depending on its specific shape and classification. The number of sides in a polygon determines its unique properties and characteristics.
Polygons are widely used in modern applications across various industries. Let’s explore how they are utilized in Architecture and Design as well as Digital Graphics.Architecture And Design
In Architecture, polygons are fundamental in designing structures. They help create geometrically precise blueprints for buildings. – Blueprints are drafted using polygons for accurate measurements. – Structural components like facades often incorporate polygonal shapes.Digital Graphics
Digital Graphics heavily rely on polygons for creating 3D models and visual effects. 1. 3D models are constructed using polygons for detailed representations. 2. Special effects in movies and video games are achieved through polygon manipulation.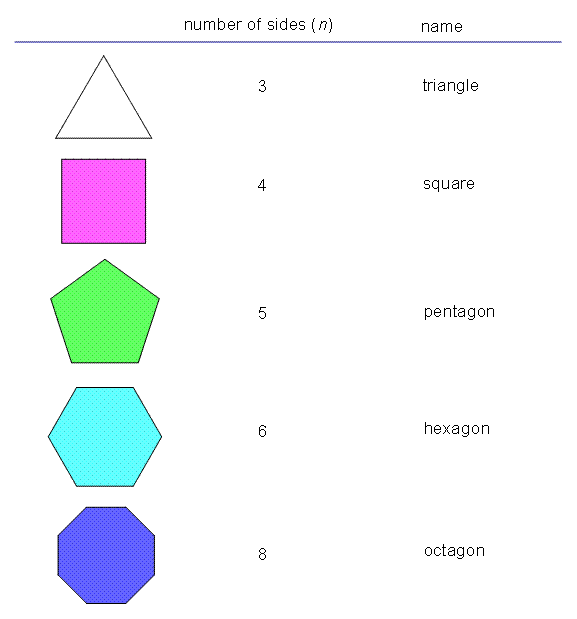
Credit: americanboard.org
Creating Your Own Polygon
Tools And Techniques
When creating a polygon, you need the right tools and techniques.
Step-by-step Guide
Follow these steps to create your own polygon:
- Choose the number of sides for your polygon.
- Decide on the length of each side.
- Use a ruler and a protractor for precision.
- Connect the sides to form your polygon.

Credit: www.flickr.com
Frequently Asked Questions
How Many Sides Does A Polygon Have?
A polygon is a closed shape with at least three straight sides. The number of sides a polygon has depends on the specific shape. For example, a triangle has three sides, a quadrilateral has four sides, and a pentagon has five sides.
In general, a polygon can have any number of sides as long as it meets the definition of being a closed shape with straight sides.
What Is The Formula To Find The Number Of Sides In A Polygon?
To find the number of sides in a polygon, you can use the formula: n = 180 x (s-2) / s, where n is the number of sides, and s is the measure of each interior angle in degrees. Alternatively, you can count the number of sides by visually inspecting the shape and counting the number of straight sides that form the shape.
What Is The Difference Between A Polygon And A Regular Polygon?
A polygon is a closed shape with at least three straight sides, while a regular polygon is a polygon with all sides and angles equal. For example, a square is a regular polygon because it has four equal sides and four right angles.
In contrast, a rectangle is a polygon, but it is not a regular polygon because it has two pairs of sides with different lengths.
What Is A Convex Polygon?
A convex polygon is a polygon where all interior angles are less than 180 degrees. This means that all the vertices of the polygon point outward, away from the interior of the shape. A convex polygon can have any number of sides, but it must meet the definition of having all interior angles less than 180 degrees.
Conclusion
Understanding the number of sides in a polygon is crucial for geometry enthusiasts. Through this post, we’ve explored the concept in depth. Remember, a polygon can have any number of sides, making it a fascinating shape to study. Keep exploring the world of polygons!